Math is everywhere. All we know is that a single math equation calculates all processes in this world. Now we will see about the Pythagoras theorem, which is a foundation for mathematics. For example, the Pythagorean theorem, simple algebra and geometry, is used to construct Egypt’s great pyramid. Greek philosopher and mathematician Pythagoras is known for the Pythagorean theorem (1900 B.C.). It has been almost 4000 years since its discovery, and 367 proofs are available for this theorem. We’ll see the following step by step.
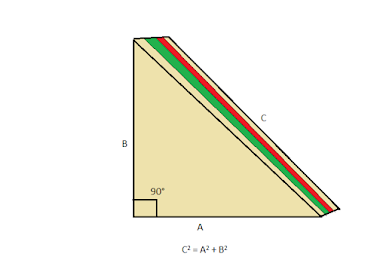
Let us assume that we have a triangle-shaped sandwich (imagine it has one right angle). Consider the length of the diagonal line(Hypotenuse) of the sandwich as C, and the other two sides Length as A and B. Pythagorean theorem states that “square of the diagonal line is equal to the sum of the square of other two sides”. It is only applicable for a right-angle triangle.i.e. C2 = A2 + B2
Right angle triangle or right triangle:
Based on the angle, three types of triangles are there—Acute-Angle, Obtuse-Angle, Right-Angle triangle. The right-angle triangle has a 90° angle opposite to the hypotenuse. The hypotenuse is the longest side compared to the other sides of a triangle.
Can we use this theorem for all triangles?
No, it is applicable only for the right triangle. Triangle has an angle of 180˚ (A+B+C=180°). We know that the Pythagoras theorem states that the right angle equals the sum of the other two angles.
i.e. A+B+C = 180˚
(one angle C=90°)
A+B+90˚ = 180˚
A+B = 90°
Therefore, the sum of the angle of the other sides of the triangle should be equal to the right angle. Hence the Pythagoras theorem is only applicable for the right-angle triangle.
What are the ways to use this theorem?
It is the most widely used theorem, nearly 4000 years. We can use this for engineering, geometry, trigonometry, physics, construction and architecture, finding signals, navigation, archery, painting, good crime scenario, construction of Egypt pyramid, sports, to find the height of mountains and tower, even for buying a television. Here we see some examples:
1. Navigation:
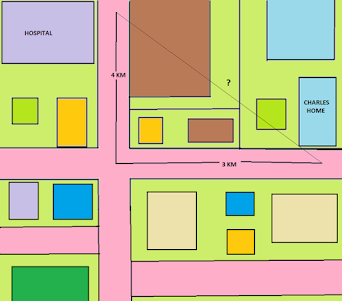
Pythagoras theorem is used to find the distance between two points. If you are in an emergency, you can use this theorem for finding the fastest route. For example, Charles has to go to the hospital. Here we see the map; imagine a right triangle in it. From the home to one end, it will be(A) 3KM, and the other side has (B)4KM. What will be the hypotenuse(C) length?
C2 = A2 + B2
C2 = 32+42
C2 = 25
C = 5KM
You can use it for the world map also.
2. Construction:
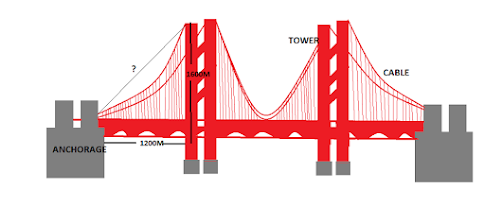
We can use this theorem to find the length. Imagine a suspension bridge with two anchorages, two towers and cables connected for the support, which seems like a right-angle triangle. Consider a horizontal line between the anchorage and the bottom of the tower that measures 1200m(A). The height of the building measures 1600m(B). What will be the cable length?
C2 = A2 + B2
C2 = 12002+16002
C = 2000m
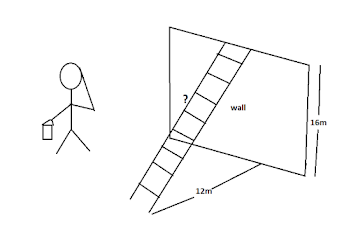
3. Painting a wall:
We have to use the ladder for painting a lengthy wall so, we have to calculate the length of the ladder to use. For example, consider a wall with a height of 16m(A), and the distance between the wall and ladder is 12m(B). What is the length of the ladder?
C2 = A2 + B2
C2 = 162+122
C = 20
What are all the things that proved the existence of the Pythagorean theorem?
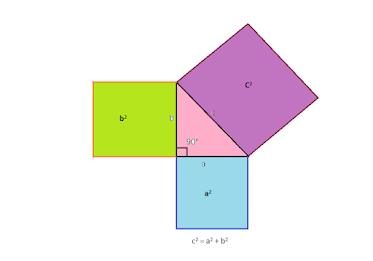
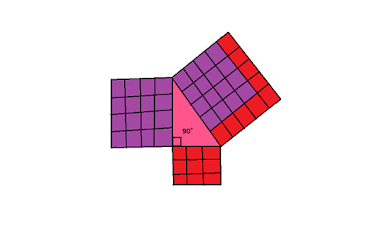
Consider four identical right-angle triangles. Arrange it in a square shape. image-1.1 has the area of c2 (violet), which is equal to the area of the other two (green and blue) small squares shown in image-2.1. It is a rearrangement of four right triangles. Therefore it has the same area.
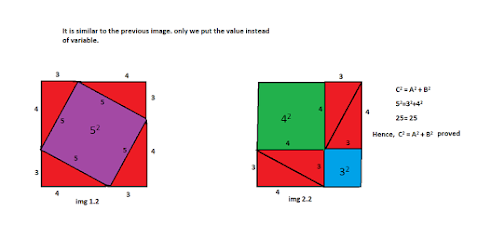
For instance, let us consider the steps mentioned above. Image 1.2 shows that it has an area of 52 (equal to 25) and image 2.2 shows the area of 32(blue) + 52(green), which is equal to the value of 25. Hence, C2 = A2 + B2 proved.
Pythagorean triples:
The integer (k) that satisfies the Pythagorean theorem is called Pythagorean triples. The integer should be positive K > 0.
The most common Pythagorean triples are,
3 – 4 – 5
5 -12-13
7 – 24- 25
9 – 40- 41
20-21 – 29
Discover more from Aristoscienceworld
Subscribe to get the latest posts sent to your email.